近日，同济大学工程风险研究团队张冬梅教授、黄忠凯助理教授、曾念晨硕士生和英国布鲁内尔大学Sotirios Argyroudis教授、伦敦大学学院Stergios-Aristoteles Mitoulis教授在《Engineering》期刊上发表了题为“Resilience Models for Tunnels Recovery after Earthquakes”的研究论文，报道了一种融合专家经验与物理机制的隧道功能恢复模型及其不确定概率量化方法。

作为城市生命线工程，隧道受到地震、火灾、洪水等突发事件的严峻威胁，加之结构老化与邻近施工扰动等影响因素，对隧道韧性构成严峻挑战。可靠的灾后结构性能恢复模型是实现韧性评估的核心基础，为此，本研究以地震灾害为例，充分考虑盾构隧道震后修复工程实践，提出了隧道震后性能恢复量化方法，实现了隧道抗震韧性定量评估。

首先，针对盾构隧道震后修复过程设计了详细调研问卷，获取了震后决策时间、修复措施持续时间、修复工序、震后交通承载力及修复费用等关键指标；基于此，确定了震后修复过程时间变量的最佳概率分布类型（图1）；然后，考虑不同损伤等级下修复措施及修复工序的不确定性，通过蒙特卡洛模拟构建了相应的震后性能恢复模型（图2）；最后，通过易损性曲线考虑不同震动强度（PGA）下的隧道结构损伤概率，以损伤概率为权重对不同损伤状态下的结构性能加权求和构建了韧性曲线（图3），以此量化了隧道抗震韧性，揭示了不同地震强度下隧道抗震韧性的概率演化规律（图4）。本研究为基于韧性的震后修复决策制定和优化提供了系统的理论框架和方法支撑。

致谢

衷心感谢各位审稿专家的宝贵意见，让本研究更加完善；同时特别感谢参与问卷调研的专家学者，其专业见解和耐心反馈为研究提供了重要支撑；这项研究的顺利完成，离不开隧道五室的支持，以及周文鼎博士、甘彬博士生等团队成员在问卷设计中的辛勤付出；在此，向每一位为本研究贡献力量的同仁致以诚挚的谢意

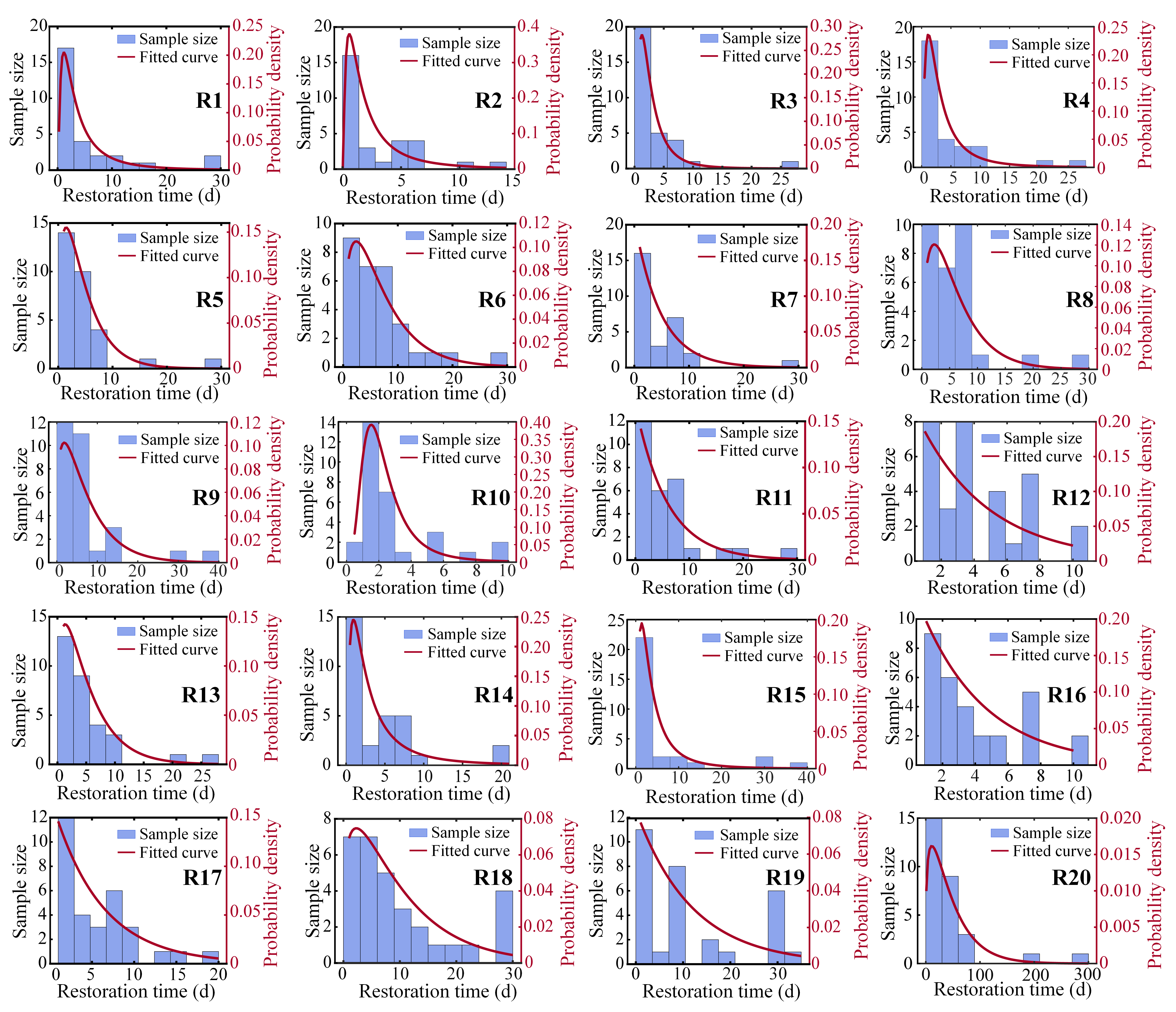
图1 修复任务最短持续时间直方图及最佳拟合概率密度函数

图2 基于最短修复时间的阶梯型结构性能恢复模型：(a)轻微损伤；(b)中等损伤；(c)严重损伤工况；(d)完全损伤

图3 不同PGA下基于最短修复时间的概率韧性曲线：(a) 0.2g；(b) 0.5g；(c) 1.0g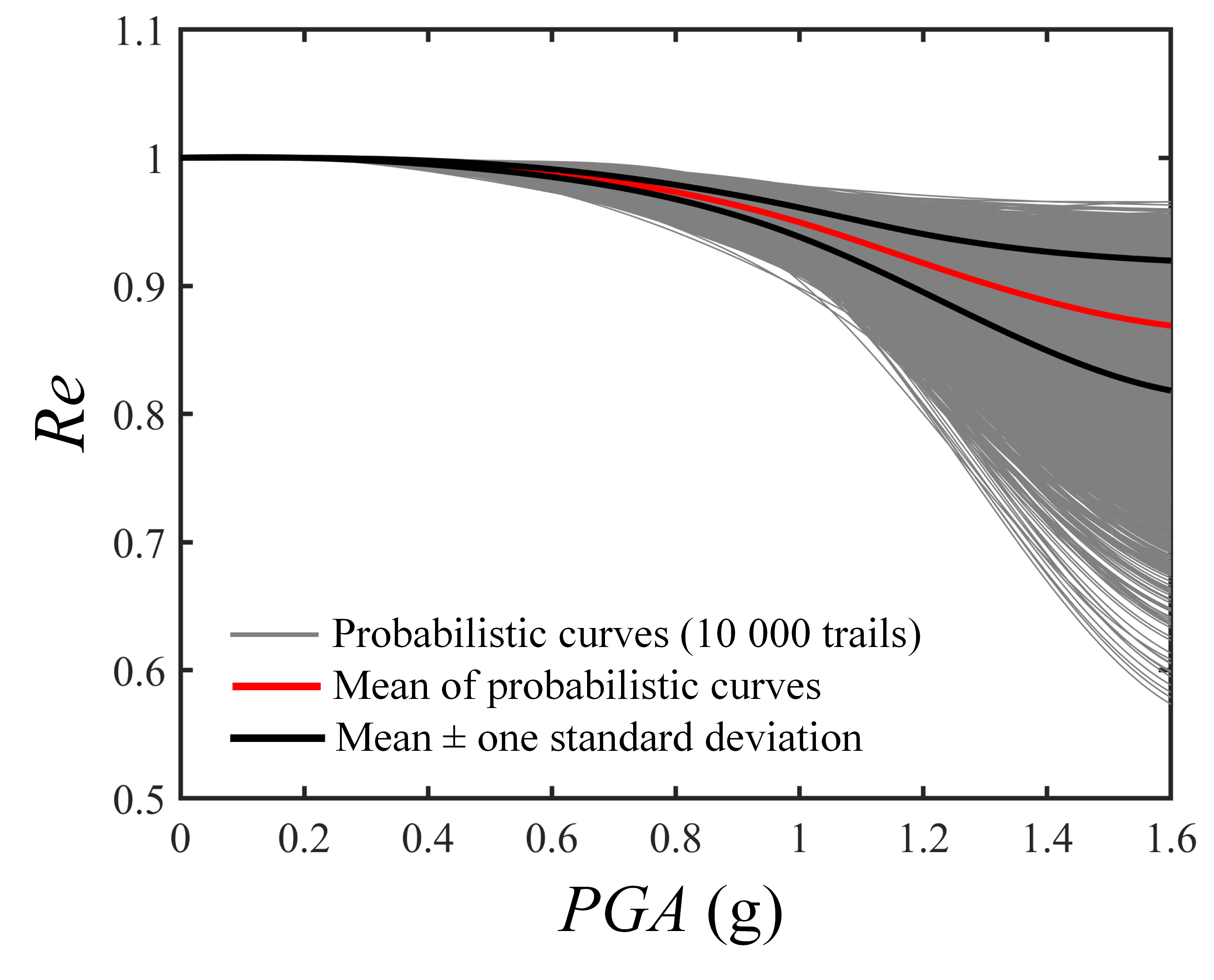

(a)

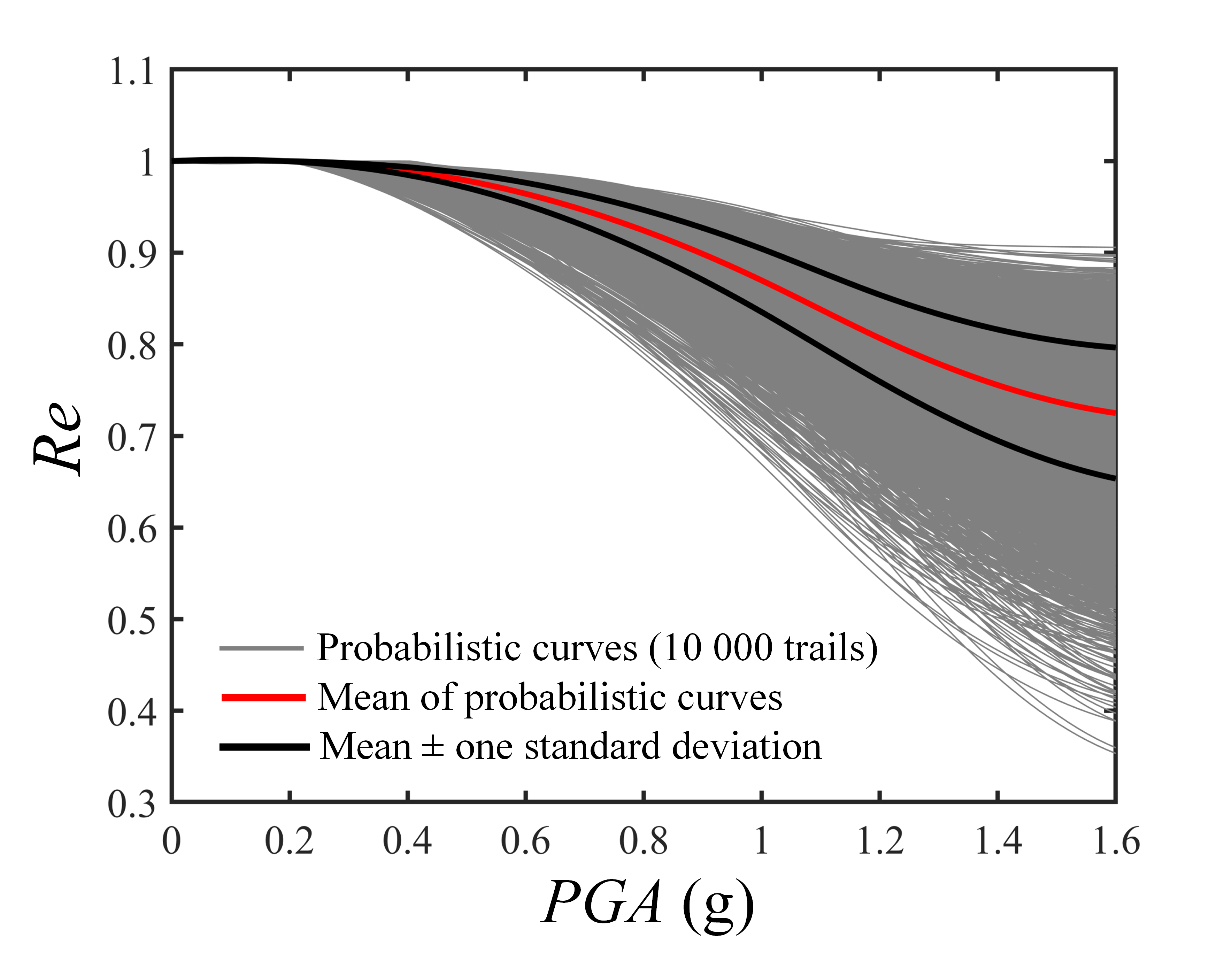
(b)

图4 抗震韧性概率演化规律： (a)最短修复时间场景 ；(b)最长修复时间场景

第一作者

黄忠凯 助理教授 

主要从事复杂条件下盾构隧道结构安全评价与韧性提升等研究  

邮箱：5huangzhongkai@tongji.edu.cn

第二作者

曾念晨 硕士 

主要从事地下空间结构韧性评价与提升研究

邮箱：2330659@tongji.edu.cn

第三作者和通讯作者

张冬梅 教授 

主要从事隧道结构安全评价与控制、隧道结构韧性提升理论等领域研究

邮箱：dmzhang@tongji.edu.cn

第四作者

Sotirios Argyroudis 教授 

主要从事城市基础设施在多灾害与气候变化条件下的易损性、灾害风险及韧性评估方面的研究

邮箱：sotirios.argyroudis@brunel.ac.uk

第五作者

Stergios-Aristoteles Mitoulis 教授 

主要从事城市关键基础设施的可持续性、韧性和数字化方面的研究

邮箱：s.mitoulis@ucl.ac.uk

文献引用

 Z-K. Huang, N-C. Zeng, D-M. Zhang, S. Argyroudis, S-A. Mitoulis, Resilience Models for Tunnels Recovery After Earthquakes, Engineering (2025), doi: https://doi.org/10.1016/j.eng.2025.06.028

原文链接

https://doi.org/10.1016/j.eng.2025.06.028

原文二维码

撰稿：曾念晨

编辑：曾诗怡

校对：王森

审核：申轶尧